Test ACID compliance with a Ring test

A distributed graph database represents and stores data as graph structures distributed across multiple machines. If the database is ACID-compliant, it should ensure transactional reliability even across multiple servers. Distributed graph databases are frequently used for knowledge graphs, recommendation engines, fraud detection, etc. Some of the popular databases include Neo4J, AWS Neptune, ArangoDB, Dgraph by Hypermode, and more.

To test such a database we’ll introduce a test workload called the “Ring test”.

In this tutorial, you’ll learn about:

• ACID transactions,
• The ring test (a conceptual explanation),
• How to implement a ring test with a reference implementation that tests a Dgraph cluster.

Scenario

Imagine n friends organize a potluck party and decide to split the expenses equally. Each time a person spends money, they record the transaction as follows:

• An edge spent(FROM person to items) with the amount spent.
• Edges owes(FROM person to spender), indicating the amount.

For n=3 the database is initialized as:

BEGIN TRANSACTION

CREATE
(a:Person {name: "A", address: "pqr"}),
(b:Person {name: "B", address: "xyz"}),
(c:Person {name: "C", address: "mno"})

COMMIT TRANSACTION

If person A spends $30 on snacks then the following edges will be added to the graph:

• a – spent {amount: $30} -> snacks
• b – owes {amount: $10} -> a
• c – owes {amount: $10} -> a

Atomicity

An atomic transaction consisting of multiple operations is a single unit: either all operations commit successfully or none do.

Example:
A spent $60 on decor. For n=3, each person’s share is $20.

This transaction will be recorded like:

BEGIN TRANSACTION

CREATE
(party_decor:Items {uid: 12345, bought_from: "store_1", bought_on: timestamp_1}),
(a:Person) - [:Spent {amount: 60}] -> (party_decor:Items),
(b:Person) - [:Owes {expense_id: 12345, amount: 20}] -> (a:Person),
(c:Person) - [:Owes {expense_id: 12345, amount: 20}] -> (a:Person)

COMMIT TRANSACTION

Either all three statements in the transaction are committed or all fail. If the above transaction isn’t atomic, and if first three operations complete successfully but not the last one, then A ends up paying more than their fair share.

Consistency

For database systems, consistency refers to the data integrity rules. Any data written to the database must be valid according to all defined rules, including constraints, cascades, triggers, and any combination.

Example:
Assuming that the database is configured so it cascades deletions from expense to owed entries. If A returns the decorations bought before and buys new decorations from another store for $30, then the older expense and owed edges should be deleted.

BEGIN TRANSACTION
MATCH () - [e:Spent] -> (i:Items)
WHERE i.uid = 12345
DELETE e
COMMIT TRANSACTION

BEGIN TRANSACTION
CREATE
(party_decor:Items {uid: 12346, bought_from: "store_2", bought_on: timestamp_2}),
(a:Person) - [:Spent {amount: 30}] -> (party_decor:Items),
(b:Person) - [:Owes {expense_id: 12346, amount: 10}] -> (a:Person),
(c:Person) - [:Owes {expense_id: 12346, amount: 10}] -> (a:Person)
COMMIT TRANSACTION

If any of the older edges survive the first transaction, it violates the data integrity rules and the transaction wasn’t consistent.

Isolation

Database transactions can be executed concurrently (e.g. multiple transactions reading and writing to the same data at the same time). Isolation means that transactions must appear to run in isolation without interference from other transactions. There are many levels of isolation, going from low to high level of strictness, Read uncommitted, Read committed, Repeatable read, Snapshot isolation, Serializability.

Example:
B spends $150 on beverages and C spends $50 on groceries concurrently. Both transactions update the owed edges and they shouldn’t corrupt or overwrite each other. (The pseudocode highlights the simplification logic where the owed edges are constantly updated on every transaction.)

-- They are concurrent transactions

BEGIN TRANSACTION

CREATE
(beverages:Items {uid: 12347, bought_from: "store_1", bought_on: timestamp_3}),
(b:Person) - [:Spent {amount: 150}] -> (beverages:Items)

MATCH (p) - [o:Owes] -> (q:Person)
WHERE q.name = B
SET o.amount += 50

MATCH (p:Person) - [o:Owes] -> (q)
WHERE p.name = B

if (o.amount - 50 > 0) {
    SET o.amount -= 50
}
else if (o.amount - 50 = 0) {
    DELETE o
}
else {
    CREATE (q) - [oo:Owes {amount: 50 - o.amount}] -> (p)
    DELETE o
}

COMMIT TRANSACTION

BEGIN TRANSACTION

CREATE
(beverages:Items {uid: 12348, bought_from: "store_2", bought_on: timestamp_4}),
(c:Person) - [:Spent {amount: 45}] -> (beverages:Items),
MATCH (p) - [o:Owes] -> (q:Person)
WHERE q.name = C
SET o.amount += 15

MATCH (p) - [o:Owes] -> (q:Person)
WHERE p.name = C

if (o.amount - 15 > 0) {
    SET o.amount -= 15
}
else if (o.amount - 15 = 0) {
    DELETE o
}
else {
    CREATE (q) - [no:Owes {amount: 15 - o.amount}] -> (p)
    DELETE o
}

COMMIT TRANSACTION

Durability

Once a transaction is committed, it should continue to exist even in the face of hardware failures.

Example:
C spends $10 on cups. This transaction once committed should be durable.

BEGIN TRANSACTION

CREATE
(cups:Items {uid: 12349, bought_from: "store_1", bought_on: timestamp_4}),
(c:Person) - [:Spent {amount: 10}] -> (cups:Items),
(a:Person) - [:Owes {amount: 3.3}] -> (c:Person),
(b:Person) - [:Owes {amount: 3.3}] -> (c:Person)

COMMIT TRANSACTION

BEGIN TRANSACTION

MATCH (p) - [e:Spent] -> (i:Items)
WHERE e.uid=12349
RETURN p.name, e.amount

COMMIT TRANSACTION

The search query should return a single result with values - C, $10.

Ring test

This is a simple way to test ACID-compliance in graph databases, which we call a Ring test.

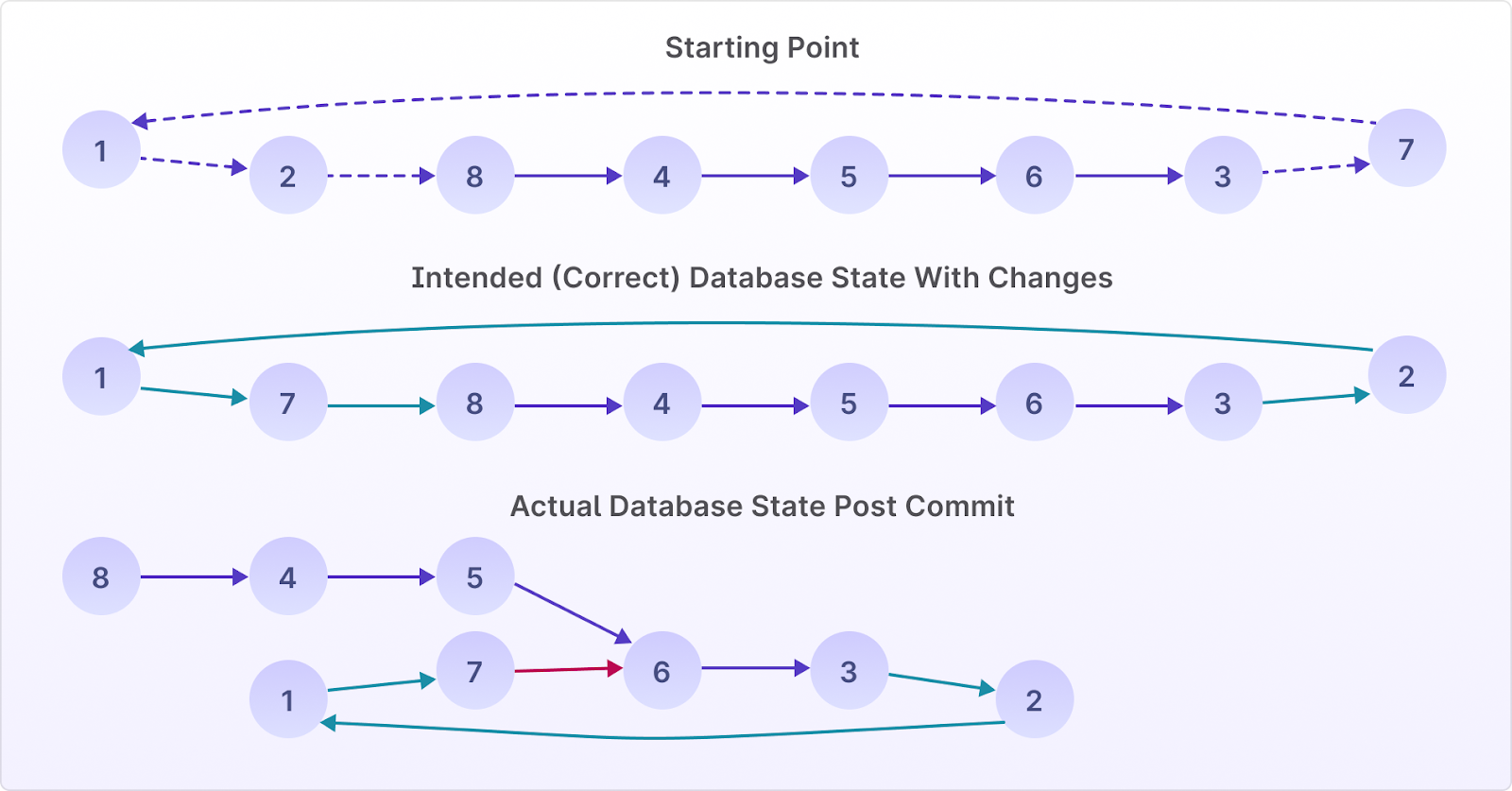
A ring test starts with n nodes forming a ring such that all the nodes can be visited in n-1 steps. Two random nodes in the graph are swapped by deleting their old connections and creating new ones.

For example, in the image below, the nodes 1 and 3 are swapped.

For such a transaction, we want to ensure that,

• No nodes are deleted.
• No new nodes are added.
• The total number of edges in the graph remains constant.
• The ring is maintained after the transaction.

All of the above can be converted into test properties for a ACID-compliant database.

Here’s how to implement a ring test.

Create a ring with n nodes

# Generate a random number of nodes
num_nodes ← random_number(min: 3, max: 10)

# Set the number of edges in a ring
num_edges ← num_nodes

# Create graph data structure
graph_data ← empty list

FOR i FROM 0 to num_nodes
    IF i == num_nodes-1:
	APPEND {name: i, friend: 0} TO graph_data
    ELSE:
    	APPEND {name: i, friend: i+1} TO graph_data

# Create graph data schema
schema = """
    name: string
    counter: int
    friend: [uid]
    """

client ← get_client_distributed_graph_db()
client.set_schema(schema)

# Add graph data (this function will execute create queries)
add_graph_data(client, graph_data)

Pre-transformation ring check

Before running the transformations on the graph, check that the ring exists.

# check for a ring before swapping
FUNCTION check_ring(edges):

    FOREACH edge(start, end) in edges:
        original_node ← start
        next_node ← end

        // Traverse through all edges in the graph
        FOR e_index from 0 to length(edges) - 2:
            // Find the next edge whose first node matches the next_node
            idx_of ← first index i in edges such that edges[i].first == next_node
            next_node ← edges[idx_of].second

        // After full traversal, check if we returned to the starting node
        if original_node != node_next:
            return False

    return True

Concurrent ring transformations

In a single ring transformation,

• The graph is queried for all the triplets, i.e. (0, 1, 2), (1, 2, 3), ... as per the above example graph.
• Two random indices are chosen without replacement and the nodes at the center of the two triplets are swapped.
• Transaction is committed.

When implementing the ring test, hundreds of ring transformations should be executed concurrently to effectively test the database.

# Parse triplets from the graph
FUNCTION get_triplets(client):

query = <query to get nodes with friends 2 level deep>
results = client.execute_query(query)
triplets = parse_triplets(results)

# triplets
[ {prev: 0, curr: 1, next: 2}, {prev: 1, curr: 2, next: 3}, ...]

RETURN triplets

FUNCTION transform_ring(triplets):
    # Pick two random indices
    nodes = [i FROM 0 TO num_nodes]
 
    index_1 = random_number_from_list(nodes)
    nodes.remove(index_1)
    index_2 = random_number_from_list(nodes)

    triplet_1 = triplets[index_1]
    triplet_2 = triplets[index_2]

    # complex logic to delete edges and create new edges
    # to delete edges: there are 2 cases
    # case 1: the nodes to be swapped aren't adjacent
    # case 2: the nodes to be swapped are adjacent (fewer edges to delete)

    edges_to_delete = [...]
    edges_to_create = [...]
    
    commit transaction

Check if the ring is maintained

Periodically after running some ring transformations, check if the ring is still maintained. The code to check for a ring is the same as the pre-transformation ring check. Optionally, you can also check that no new nodes are added or no nodes are deleted.

What the ring test checks

The ring test checks for ACID compliance by

• Ensuring atomicity when deleting and creating edges.
• Ensuring isolated execution of transactions during concurrent execution.
• Ensuring that committed transactions are durably stored by comparing the ring status locally and in the database. The easiest way to do this is to keep a local set of counters for each node, and increment the local counter as well as a counter in the database every time a transaction returns as “successful.” If the counter in the local file is higher than the one in the database, it means a successful transaction got lost somehow.

Reference implementation

Dgraph, a distributed graph database, guarantees true ACID transactions:

“Dgraph provides true ACID transactions, and does not impose limitations on what can be in a transaction: a transaction can involve multiple predicates, multiple nodes, multiple keys and even multiple shards.”

Our ring test implementation tested this guarantee.

With our Test Composer framework, we run the ring test in multiple parallel simulations to find rare bugs as quickly as possible.

Here’s the triage report that shows the failing assertion which is an ACID-compliance violation. Additionally, here’s the multiverse map of the test run that shows each simulation as a branch in the tree and points in time when an assertion failed.

Here’s an illustration of one of the failing cases we found:

Ring test is a relatively simple but powerful workload to expose any transaction level ACID violations in your distributed graph database and now you can find them with this workload.